Pytorchで多値分類（IRISデータセット）

Pytorchで多値分類やってみた。

ライブラリインポート

必要なライブラリをインポートする。

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torchinfo import summary
from torchviz import make_dot
import torchvision.datasets as datasets
import torchvision.transforms as transforms
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

データセット構築

2値分類とほぼ同じ。

2次元以上になると、データの可視化が困難なので、とりあえず入力をsepal_lengthとpetal_lengthの2つにしておく。

iris = load_iris()

inputs = iris.data[:,[0,2]]
labels = iris.target

train_inputs_np, test_inputs_np, train_labels_np, test_labels_np = \
  train_test_split(inputs, labels, train_size=100, test_size=50, random_state=0)

# 散布図の表示
x_0 = train_inputs_np[train_labels_np == 0]
x_1 = train_inputs_np[train_labels_np == 1]
x_2 = train_inputs_np[train_labels_np == 2]

plt.scatter(x_0[:,0], x_0[:,1], marker='x', c='k', label='0 (setosa)')
plt.scatter(x_1[:,0], x_1[:,1], marker='o', c='b', label='1 (versicolour)')
plt.scatter(x_2[:,0], x_2[:,1], marker='^', c='m', label='2 (virginica)')
plt.xlabel('sepal_length')
plt.ylabel('petal_length')
plt.legend()
plt.show()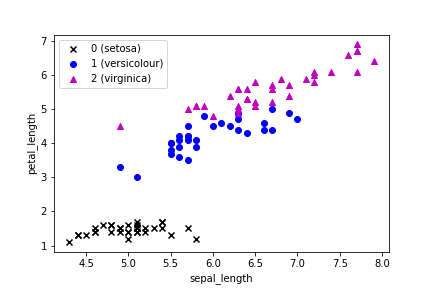

Tensorに変換しておく。ラベルは後のCrossEntropyLoss関数の関係でLong型にしなければならない。

train_inputs = torch.tensor(train_inputs_np).float()
train_labels = torch.tensor(train_labels_np).long()
test_inputs = torch.tensor(test_inputs_np).float()
test_labels = torch.tensor(test_labels_np).long()

モデル構築

多値分類ではSoftmax関数を用いるが、損失関数として用いるCrossEntropyLoss関数に含まれるため、モデルの定義では出てこない。

class Net(nn.Module):
    def __init__(self, n_input, n_output):
        super().__init__()
        self.l1 = nn.Linear(n_input, n_output)

    def forward(self, x):
        x1 = self.l1(x)
        return x1

損失関数と最適化関数定義

net = Net(2, 3)                                   # インスタンスの生成
criterion = nn.CrossEntropyLoss()                 # 損失関数： 交差エントロピー関数
lr = 0.01                                         # 学習率
optimizer = optim.SGD(net.parameters(), lr=lr)    # 最適化関数: 勾配降下法

計算グラフ

とりま計算グラフを出しておく。

outputs = net(train_inputs)                                # とりま一回計算
loss = criterion(outputs, train_labels)                    # とりま一回損失計算
g = make_dot(loss, params=dict(net.named_parameters()))
display(g)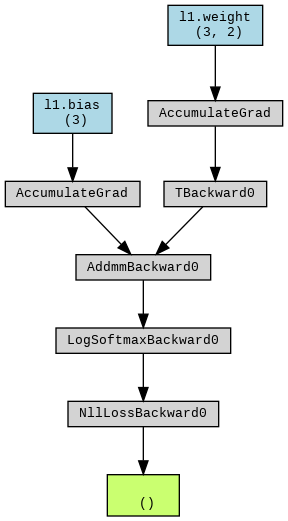

ループを回す

total_epoch = 10000                     # epoch数
log = np.zeros((0,5))                   # 損失・精度記録用
for epoch in range(total_epoch):

    # 学習フェーズ
    optimizer.zero_grad()                                                       # 勾配値初期化
    train_outputs = net(train_inputs)                                           # 予測計算
    train_loss_t = criterion(train_outputs, train_labels)                       # 損失計算
    train_loss_t.backward()                                                     # 勾配計算
    optimizer.step()                                                            # パラメータ更新
    train_loss = train_loss_t.item()                                            # 損失の保存(スカラー値の取得)
    train_predicted = torch.max(train_outputs, 1)[1]                            # 予測ラベル選択
    train_acc = (train_predicted == train_labels).sum()  / len(train_labels)    # 精度計算

    # 検証フェーズ
    with torch.no_grad():
        test_outputs = net(test_inputs)                                         # 予測計算
        test_loss_t = criterion(test_outputs, test_labels)                      # 損失計算
        test_loss =  test_loss_t.item()                                         # 損失の保存（スカラー値の取得） 
        test_predicted = torch.max(test_outputs, 1)[1]                          # 予測ラベル選択
        test_acc = (test_predicted == test_labels).sum() / len(test_labels)     # 精度計算
    
    # 10回ごとに途中経過を記録する
    if (epoch % 10 == 0):
        print (f'Epoch [{epoch}/{total_epoch}], loss: {train_loss:.5f} acc: {train_acc:.5f} val_loss: {test_loss:.5f}, val_acc: {test_acc:.5f}')
        vals = np.array([epoch, train_loss, train_acc, test_loss, test_acc])
        log = np.vstack((log, vals))

結果

損失

plt.plot(log[:,0], log[:,1], 'b', label='train')
plt.plot(log[:,0], log[:,3], 'k', label='test')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend()
plt.show()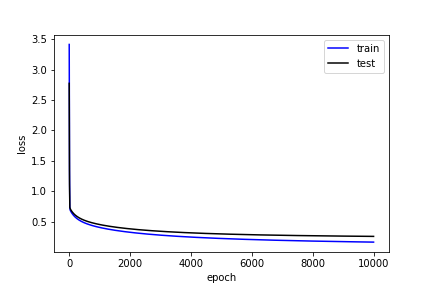

精度

plt.plot(log[:,0], log[:,2], 'b', label='train')
plt.plot(log[:,0], log[:,4], 'k', label='test')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.legend()
plt.show()

決定境界

決定境界の描き方がわからないから、グラフ上の格子点で確率出して等高線表示してみる。

# 格子点作成
x = np.arange(4, 7.51, 0.05)
y = np.arange(0.5, 6.51, 0.05)
X, Y = np.meshgrid(x, y)

# 予測計算
p = np.reshape(np.stack((X, Y), axis=-1), (-1,2))
pt = torch.tensor(p).float()
with torch.no_grad():
  o = net(pt)

# softmax関数で確率算出
softmax = nn.Softmax(dim=1)
k = softmax(o)

# 等高線の高さデータに変換
z0 = k[:,0]
z1 = k[:,1]
z2 = k[:,2]

Z0 = np.reshape(z0.data.numpy(), (X.shape[0], X.shape[1]))
Z1 = np.reshape(z1.data.numpy(), (X.shape[0], X.shape[1]))
Z2 = np.reshape(z2.data.numpy(), (X.shape[0], X.shape[1]))

#等高線描画
plt.contourf(X, Y, Z0, 10, cmap='Greens', alpha=0.3)
plt.contourf(X, Y, Z1, 10, cmap='Blues', alpha=0.3)
plt.contourf(X, Y, Z2, 10, cmap='Reds', alpha=0.3)

# 散布図描画
x_0 = test_inputs_np[test_labels_np == 0]
x_1 = test_inputs_np[test_labels_np == 1]
x_2 = test_inputs_np[test_labels_np == 2]
plt.scatter(x_0[:,0], x_0[:,1], marker='x', c='g', label='0 (setosa)')
plt.scatter(x_1[:,0], x_1[:,1], marker='o', c='b', label='1 (versicolour)')
plt.scatter(x_2[:,0], x_2[:,1], marker='^', c='r', label='2 (virginica)')

# グラフ描画
plt.xlabel('sepal_length')
plt.ylabel('petal_length')
plt.legend()
plt.show()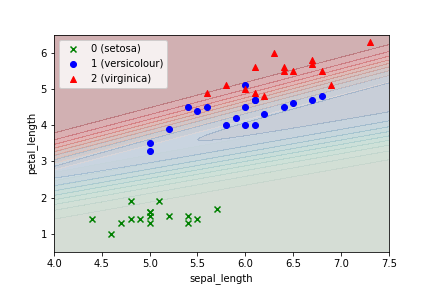

赤と青の境界が明確でなく、精度が上がらないのはこのあたりが原因か。ただ、人でもこのあたりの分類は不可能だろう。

おまけ

でたらめなデータ増やして、隠れ層とニューロン増やしてみたら、複雑な境界も引けた。

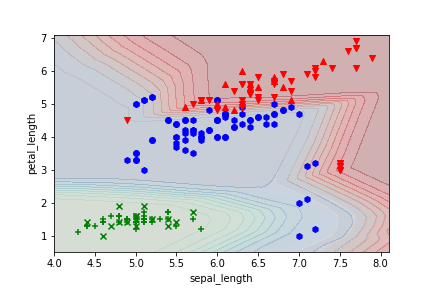
隠れ層や各ニューロンの数をどうするかは悩ましいところだが、指針としては以下のようなものがあるようだ。直感的にはわかりやすい。